ANGLES IN A POLYGON
CONTENT
- Definition of Polygons
- Types Of Polygons
- Sum of Interior Angles in a Polygon
- Sum of Exterior Angles in a Polygon
Definition of Polygons
A closed plane figure bounded by straight lines (edges) is called a polygon. The number of sides of a polygon determines its names. The table below describes the names of polygons according to the number of their sides:
Types Of Polygons
1. Convex Polygon:
A convex polygon has all its interior angles pointing outwards. No angle is pointing inwards. Each internal angle of a convex polygon is always less than 1800. A polygon is convex if any line segment joining any two points on it stays inside the polygon itself. Examples of convex polygons are shown below:
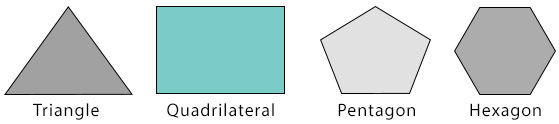
2. Concave (Re-entrant) Polygon:
If there is any internal angle greater than 180°, the angle points inwards and the polygon becomes concave.
You are viewing an excerpt of this lesson. Subscribing to the subject will give you access to the following:
- NEW: Download the entire term's content in MS Word document format (1-year plan only)
- The complete lesson note and evaluation questions for this topic
- The complete lessons for the subject and class (First Term, Second Term & Third Term)
- Media-rich, interactive and gamified content
- End-of-lesson objective questions with detailed explanations to force mastery of content
- Simulated termly preparatory examination questions
- Discussion boards on all lessons and subjects
- Guaranteed learning
ClassHall Instructor
Ezimeruwe Oghenekaro
Halima Ahmadu
Sadiq Barau