GRAVITATIONAL FIELD
CONTENT
- Gravitational Force between Two Masses (Newton’s Law of Universal Gravitation)
- Gravitational Potential Vg
- Escape Velocity V0
- Satellites and Parking Orbits
- Energy of the Satellite
- Kepler’s Laws
Gravitational Force between Two Masses (Newton’s Law of Universal Gravitation)
A gravitational field is a region of space surrounding a body that has the property of mass. Sir Isaac Newton, in 1666, propounded the universal law of gravitation.
The law states that, ”the force of attraction between two given particles of masses M and m is directly proportional to the product of the masses and inversely proportional to the square of their distance of separation”.
Mathematically,
\(F_g ∝ Mm \quad and \quad F_g ∝ \frac{1}{r^2} \\ ∴ F_g ∝ \frac{Mm}{r^2} \\ \)
\(∴ F_g = \frac{GMm}{r^2}\) ——-(1)
Hence, \(G = \frac{F_gr^2}{Mm} \)
Where Fg is the gravitational force in Newton,N,
Gis the universal or gravitational constant of value 6.7 × 10-11 and expressed in Nm2/kg2
The gravitational field strength, also called acceleration due to gravity, ‘g’ is given by:
\(g = \frac{F_g}{m} \) ——-(2)
But \(F_g = \frac{GMm}{r^2} \\ ∴ g = \frac{GMm}{r^2} \\÷ m = \frac{GMm}{r^2} \times \frac{1}{m} \)
Hence, \(g = \frac{GM}{r^2} \) ——-(3)
This is the relationship between gravitational constant G and acceleration due to gravity g.
Therefore, we define gravitational field strength ‘g’ as force per unit mass. It is a vector quantity.
Gravitational Potential Vg
The gravitational potential Vg at a point is the work done in taking a unit mass from infinity to that point on the surface of the earth.
\(V_g = gr \) ——-(4)
\(V_g = \frac{GM}{r^2} \times r \)
∴ \( V_g = \frac{GM}{r} \) ——-(5)
Where M is the mass of the earth and r is the radius of the earth of value 6.4 × 106m or 6400km
At any point, distance r from the centre of the earth, the gravitational potential experienced by a body of mass m is given by:
\(∴ V_g = −\frac{Gm}{r} \) ——-(6)
Since the potential at infinity is taken to be zero. (i.e, ∆potential \(= 0 -V_g = -V_g = -\frac{Gm}{r} \)
The negative sign indicates that potential at infinity is higher than the potential close to the mass, that is, Vg decreases as r increases.
Escape Velocity V0
Consider a rocket of mass m placed at the centre of the earth’s surface O. If it is fired from that point so that it just escapes the earth’s gravitational field, it has a kinetic energy, k.e given as:
\(k.e = \frac{1}{2}mV_0^2 \) ——-(7)
But work is done(WD) in taking this rocket to a distance R so great that the gravitational field is negligibly weak.
∴ Work done \(= mg × distance\)
This work done must be equal to the kinetic energy of the rocket at the point of take off
Work done \(= \frac{1}{2}mV_0^2 \)
∴ Work done \(= mg × R = mgR\)
but gravitational intensity \(g = \frac{GM}{R^2} \)
Work done \(= m \Big (\frac{GM}{R^2} \Big ) R\)
Work done \(= \frac{GMm}{R}\)
But k.e = WD
\(∴\frac{1}{2}mV_0^2 = \frac{GMm}{R} \\ ∴ V_0^2 = \frac{2GM}{R}\)
∴ \(V_0 = \sqrt{\frac{2GM}{R}}\) ——-(8)
But \(gR = \frac{GM}{R}\)
Hence, \(V_0 = \sqrt{2gR}\) ——-(8)
We thus define the escape velocity V0 as the velocity which is sufficient enough for a body to just escape the earth’s gravitational field.
Since g = 9.8m/s2, and R = 6,400,000m
Thus \(V_0 = \sqrt{2 \times 9.8 \times 6.4 \times 10^6} \\ = 11,200m/s (40,320km/h)\)
EVALUATION
- State Newton’s law of gravitation.
- Define escape velocity.
- Write down the mathematical expression for :
- i. Gravitational force. ii. Gravitational potential.
Worked Examples
1. Calculate the gravitation force of attraction between two planets of masses 1024kg and 1027kg separated by a distance of 1020 (G = 6.67 × 10-11).
Solution:
\(F = \frac{Gm_1m_2}{r^2} \\ = \frac{6.67 \times 10^{-11} \times 10^{24} \times 10^{27}}{(10^{20})^2} \\ = 6.67N \)
2. Find the gravitational force between a proton and an electron if their distance of separation is 10-10m. (mp = 1.67 × 10-27kg, me = 9.11 × 10-31kg
Solution:
\(F = \frac{Gm_1m_2}{r^2} \\ = \frac{6.67 \times 10^{-11} \times 1.67 \times 10^{-27} \times 9.11 \times 10^{-31}}{(10^{-10})^2} \\ = 1.01 \times 10^{-47}N \)
Satellites and Parking Orbits
Satellites are bodies, natural or artificial which move in orbits around the moon or planets.Artificial satellites are made by man.
Consider a satellite of mass m moving round the earth of mass M in an orbit as shown below:
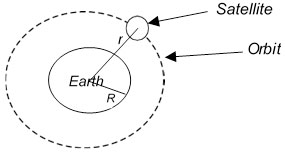
If R is the radius of the earth, r is the radius of the orbit and v is the velocity with which the satellite is moving,
We have that centripetal force (due to the satellite) = gravitational force (due to the earth)
\(∴ \frac{mv^2}{r} = \frac{GMm}{R^2} = mg \\ ∴ \frac{mv^2}{r} = mg \\ ∴ v^2 = gr \)
Hence, \(v = \sqrt{gr} \) ——-(9)
To get the time for one complete revolution, i.e, period, we use
\(speed = \frac{distance}{time} \)
Therefore, the period T is given as:
\(T = \frac{\text{length of circumference}}{\text{speed}} = \frac{2\pi R}{v} \)
But \(v = \sqrt{gr} \\ ∴ T = \frac{2 \pi R}{\sqrt{gR}} \)
By squaring both sides, we have,
\(T^2= \frac{4 \pi^2 R^2}{\sqrt{gR}} = \frac{4 \pi^2 R}{g} \)
Hence, \(T = 2\pi \sqrt{\frac{R}{g}} \) ——-(10)
Since R = 6400km and g = 9.8m/s2, therefore, T = 5077.58s = 84.6mins. This is the period for an artificial satellite in the orbit above the earth.
If the period of the satellite in its orbit is equal to the period of the earth about its axis, which is 24hours, the satellite will stay at the same place above the earth as the earth rotates. Such orbit is called ‘’Parking Orbit’’.
Now, \(\frac{mv^2}{R} = \frac{GMm}{R^2}\)
But \(GM = gr^2 (from \frac{GM}{r} = gr = V_g)\)
We have, \(\frac{mv^2}{R} = \frac{mgr}{R^2}\)
Now, multiplying through by R/m, we have:
\(v^2 = \frac{gr^2}{R}\)
Again, \(v = \frac{2 \pi R}{T}\)
\(∴ (\frac{2 \pi R}{T})^2 = \frac{gr^2}{R} \\ \frac{4 \pi^2 R^2}{T^2} = \frac{gr^2}{R}\)
By simplification,
\(R = \sqrt[3]{\frac{gT^2R^2}{4\pi^2}}\) ——-(11) Radius of orbit
Hence, the length the satellite is above the earth surface \(l = R_{orbit} -R_{earth}\)
EVALUATION
- State the relationship between radius of the orbit and the radius of the earth.
- What is a satellite?
- What is the value of g at the orbit?
Energy of the Satellite
Supposing a satellite of mass m is revolving in an orbit of radius r round the earth of mass M with a velocity v,then it will have both kinetic and potential energies.
Recall that \(\frac{mv^2}{r} = \frac{GMm}{R^2} = mg \\ ∴ \frac{mv^2}{r} = \frac{GMm}{r^2} \)
Hence, \(v^2 = \frac{GM}{r} \)
Now, \(k.e = \frac{1}{2}mV^2 \)
Putting in the value of v2 above, we have:
\(k.e = \frac{1}{2}m \times \frac{GM}{r} = \frac{GMm}{2r} \)
Hence, \(k.e = \frac{GMm}{2r}\) ——-(12)
Also, \(p.e. = mgh = -\frac{GMm}{r}\)
∴ Total energy \(k.e + p.e = \frac{GMm}{2r}+ -\frac{GMm}{r}\)
Hence, total energy in orbit \(= -\frac{GMm}{2r}\) ——-(13)
Worked Examples
1. Find the satellite orbit above the earth’s surface if the radius of that orbit is 6.5 × 106m.
Solution:
\(l = R_{orbit} -R_{earth} \\ l = 6.5 \times 10^6 -6.4 \times 10^6 \\ = 100,000m = 100km\)
2. Determine the speed of revolution of a satellite round an orbit revolving at 85mins per revolution if the satellite is at 110km above the earth’s surface.
Solution:
\(Speed = \frac{2\pi R}{T}\)
Now, T = 85mins = 5100s,
R = radius of the orbit \(= 110km + 6400km \\ = 6510 = 6,510,000m \\Speed = \frac{2\pi \times 6510000}{5100} = 8020.3m/s\)
Kepler’s Laws
Johannes Kepler in his working with data together with Tycho Brahe, put forth three laws which described the motion of the planets across the sky.
The laws are:
- The Law of Orbits: All planets move in elliptical orbits, with the sun at one focus.
- The Law of Areas: Aline that connects a planet to the sun sweeps out equal areas in equal
- The Law of Periods: The square of the period of any planet is directly proportional to the cube of the semi-major axis of its orbit.
Kepler’s laws were derived for orbits around the sun, but they apply to satellite orbits as well.
GENERAL EVALUATION
- State the mathematical expression of Isaac Newton’s law of gravitation.
- What is the mathematical relationship between gravitational intensity and gravitational potential?
- State the Kepler’s laws.
- Considering a rocket launched from the earth’s surface, show that the velocity of escape V0 is given by: \(V_0 = \sqrt{2gR}\)
- Estimate the possible gravitational force between the earth and the moon at 4 × 108m apart if their masses are 6 ×1024kg and 7 ×1022kgrespectively.
- NEW: Download the entire term's content in MS Word document format (1-year plan only)
- The complete lesson note and evaluation questions for this topic
- The complete lessons for the subject and class (First Term, Second Term & Third Term)
- Media-rich, interactive and gamified content
- End-of-lesson objective questions with detailed explanations to force mastery of content
- Simulated termly preparatory examination questions
- Discussion boards on all lessons and subjects
- Guaranteed learning
it was helpful
It is a good one
I really love your work
Wow 😯 very interesting
Really helped me out
Gorgeous 🥰
Wow it was helpful
You are good!