LONGITUDE AND LATITUDE

CONTENT

1. Revision of Arc Length of a Curve
2. Calculation of Distance between Two Points on the Earth; Shortest Distance between Two Points (Great Cicle Routes)
3. Nautical Mile and Time Variations

Revision of Arc Length of a Curve

Recall,

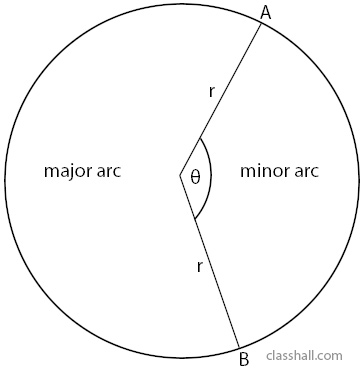
Arc length \(AB, L = \frac{θ}{360}×2πr\)   OR   Arc length \(AB, L = πr\frac{θ}{180}\)

but the angle \(θ\) is given as, \(θ=\frac{180 L}{πr}\)  or  \(\frac{360 L}{2πr}\)

Perimeter of sector \(AB = \frac{θ}{360}×2πr + 2r\)

Area of sector \(AOB = \frac{θ}{360} ×πr^2\)

Examples:

1. In the figure below, AB is a chord of the circle centre O and radius 12cm, <AOB = 100⁰. Calculate correct to 3 s.f.

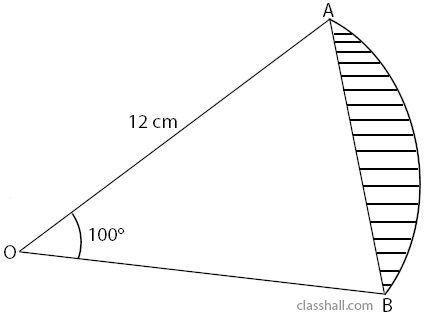
(a) The length of chord AB

(b) The length of arc ADB

(c) The perimeter of sector OADB

(d) The area of the shaded segment (Take \(π=\frac{22}{7}\))

 Solution:

(a) In the diagram, OM bisects <AOM and the chord AB.