Mensuration 2

CONTENT:

(e) Relation between the sector of a circle and the surface area of a cone.

(f) Surface area and volume of solids; (i) Cube, cuboids (ii) Cylinder (iii) Cone

(iv) Prisms (v) Pyramids.

Relation between the sector of a circle and the surface area of a cone.

If a sector of a circle AOB is cut and folded into a come as shown in the diagram below.

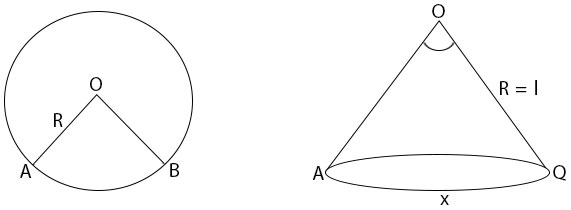
The arc AB becomes the circumference of the base of the cone. The radius R becomes the slant edge l of the cone.

∴ Arc \( AB = 2πr\)

From the above diagram.

The area of the sector = area of the curved surface of the cone

Length of arc AB = circumference of the circular base of the cone

Curved surface area of cone \( = \frac{θ}{360^o} × πl^2\)

Also, \( = \frac{θ}{360^o} × 2πl = 2πr \\ \frac{θ}{360^o} = \frac{r}{l}\)

Total surface area of cone \( = πrl = πr^2 \\ πr (l + r) \)

Example 1: Calculate in terms of π, the total surface area of a cone of base diameter 12cm and height 10cm.