MENSURATION
CONTENT
(g) Surface areas and volume of frustum of a cone and pyramid.
(h) Surface area and volume of compound shapes.
- Surface area of frustum of a cone and pyramids
- Volume of frustum of a cone and pyramid
- Surface area and volume of compound shapes
TOTAL SURFACE AREA OF FRUSTUM OF CONE AND PYRAMIDS
A frustum is the remaining part of cone or pyramid when the top part is cut off as shown below. Daily examples of frustums are buckets, lamps shades e.t.c.
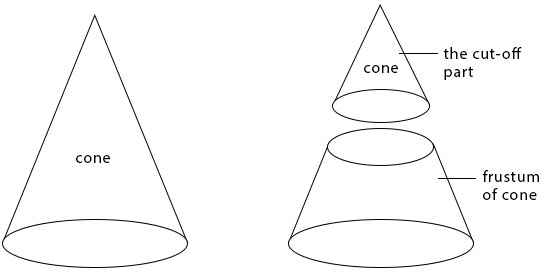
Frustum of a cone
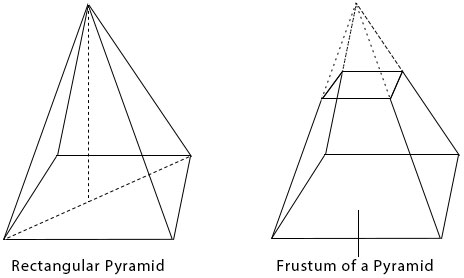
For Surface area of the frustrum of a pyramid, we sum up all areas of the faces that make up the frustum.
For Surface area of the frustum of a cone,
Total surface area of a Closed frustum = π(height × sum of radii) + area of top and base circles.
Total surface area of a Open frustum (bucket) = π(height × sum of radii) + area of circle.
Example 1:
Find the total surface area of a bucket 36cm in diameter at the top and 24cm at the bottom.
- NEW: Download the entire term's content in MS Word document format (1-year plan only)
- The complete lesson note and evaluation questions for this topic
- The complete lessons for the subject and class (First Term, Second Term & Third Term)
- Media-rich, interactive and gamified content
- End-of-lesson objective questions with detailed explanations to force mastery of content
- Simulated termly preparatory examination questions
- Discussion boards on all lessons and subjects
- Guaranteed learning
ClassHall Instructor
Ezimeruwe Oghenekaro
Halima Ahmadu
Sadiq Barau