SETS

CONTENT

1. Set Operations
2. Union of Sets
3. Intersection of Sets
4. Complement of a Set
5. Venn Diagrams
6. Application of Venn Diagram up to 3 Set Problems

Operations on Sets

The Union of Sets

The Union of Sets A and B is the Set that is formed from the elements of the two Sets A and B. This is usually denoted by “A ⋃ B” meaning A Union B. Thus A ⋃B is the Set which consists of elements of A or of B or of both A and B.

When represented using Venn diagram we have
A ⋃B

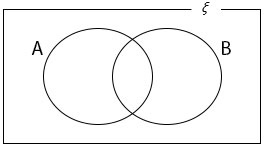
Using Set notations, the Union of two Sets A and B is solved as follows

Example 1:

Given that A = {3, 7, 8, 10}

and B = {3, 5, 6, 8, 9} then

A B= {3, 5, 6,7, 8, 9,10}

Example 2:

If A = {a, b, c, d}, B = {1, 2, 3, 4} and C = {a, 3, θ} Then A ⋃B ⋃C = {a, b, c, d,1, 2, 3, 4, θ}

Class Activity

A = {7, 8, 9, 10}, B = {8, 10, 12, 14} and C = {7, 9, 10, 14.