TRIGONOMETRY
CONTENT
(a) Basic Trigonometric Ratios: (i) Sine (ii) Cosine (iii) Tangent with Respect to Right-angled Triangles.
(b) Trigonometric Ratio of: (i) Angle 300 (ii) Angle 450 (iii) Angle 600.
Basic Trigonometric Ratios (i) Sine (ii) Cosine (iii) Tangent with respect to right-angled triangles.
These trigonometric ratios are applicable to right – angled triangle. A right – angle triangle is 900. Thus the remaining two angles add up to 900 since every triangle contains two right angles.
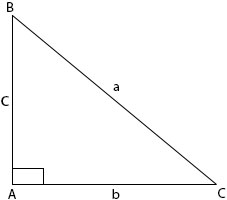
In ∆ABC, B + C = 900.
Such angles whose sum is 900 are said to be complementary angles. While capital letter are used for angles, small (lower case) letters are used for sides. Notice that the side opposite A is labelled a, the one opposite B is labelled b etc.
The side opposite the right angle is called the hypotenuse. Every right – angled triangle obeys the Pythagoras theorem. This theorem states that the square of the hypotenuse of any right angled triangle is equal to the sum of the square of the other two sides.
- NEW: Download the entire term's content in MS Word document format (1-year plan only)
- The complete lesson note and evaluation questions for this topic
- The complete lessons for the subject and class (First Term, Second Term & Third Term)
- Media-rich, interactive and gamified content
- End-of-lesson objective questions with detailed explanations to force mastery of content
- Simulated termly preparatory examination questions
- Discussion boards on all lessons and subjects
- Guaranteed learning