You must first complete Logarithms 3 before viewing this Lesson
Please sign up for the course before starting the lesson.
LINEAR INEQUALITIES
CONTENT
- Graphs of linear inequalities in two variables.
- Maximum and minimum values of simultaneous linear inequalities.
- Application of linear inequalities in real life.
- Introduction to linear programming
Graph of linear inequalities in two variables: We shall consider simultaneous inequalities.
Examples:
Show on a graph the region that contains the solution of the simultaneous inequalities
\(2x + 3y < 6,\) \(y -2x ≤ 2, y ≥ 0\)
Solution: In each case put \(y\) on one side of the inequality \(y < \frac{6 -2x}{3},\) \(y ≤ 2 + 2x\) and \(y ≥ 0\)
We shall draw the lines \(y =\frac{6 -2x}{3},\) \(y = 2 + 2x\) and \(y = 0\)
| \(x\) | -2 | 0 | 2 | 3 |
|---|---|---|---|---|
| \(y_1 = \frac{6 -2x}{3}\) | 3.3 | 22 | 0.7 | 0 |
| \(y_2 = 2 + 2x\) | -2 | 2 | 6 | 8 |
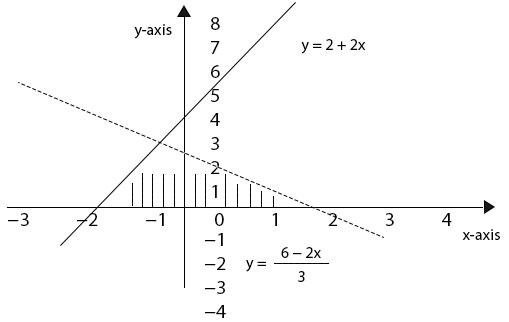
Points \(p_1(0, 0), p_2(1, 1)\) are in the solution set for the three inequalities.
You are viewing an excerpt of this lesson. Subscribing to the subject will give you access to the following:
- NEW: Download the entire term's content in MS Word document format (1-year plan only)
- The complete lesson note and evaluation questions for this topic
- The complete lessons for the subject and class (First Term, Second Term & Third Term)
- Media-rich, interactive and gamified content
- End-of-lesson objective questions with detailed explanations to force mastery of content
- Simulated termly preparatory examination questions
- Discussion boards on all lessons and subjects
- Guaranteed learning
Please sign up for the course before starting the lesson.