TRIGONOMETRY: SINE AND COSINE RULE
CONTENT
- Derivation and application of sine rule.
- Derivation and application of cosine rule.
SINE RULE
Given any triangle ABC (acute or obtuse), with the angles labelled with capital letters A, B, C and the sides opposite these angles labelled with the corresponding small letters a, b, and c respectively as shown below.
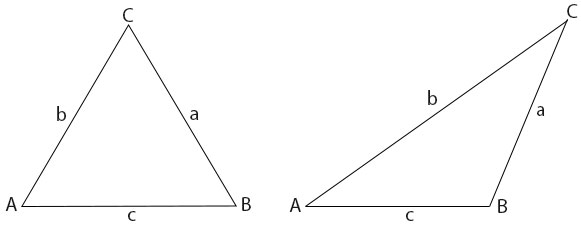
The sine rule states that;
\(\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}\)
OR
\(\frac{sinA}{a} = \frac{sinB}{b} = \frac{sinC}{c}\)
PROOF OF THE RULE
Using Acute – angled triangle
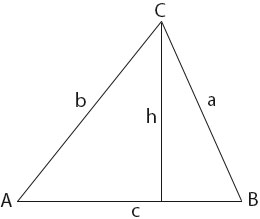
Given: Any ∆ABC with B acute.
To prove: \(\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}\)
Construction: Draw the perpendicular from C to AB.
Proof: Using the lettering in the diagram above.
\(sinA = \frac{h}{b} \\ h = bsinA …….(i) \\ sinB = \frac{h}{a} \\ h = asinB …….(ii)\)
From equation (i) and (ii)
\(bsinA = asinB \\ ∴ \frac{a}{sinA} = \frac{b}{sinB}\)
Similarly, by drawing a perpendicular from B to AC
\(\frac{a}{sinA} = \frac{c}{sinC} \\ ∴ \frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} \)
Q.E.D
Using Obtuse – angled triangle
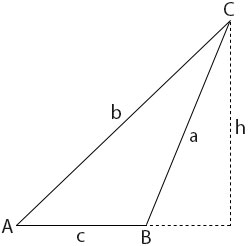
Given: any ∆ABC with B obtuse
To Prove: \(\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}\)
Construction: Draw the perpendicular from C to AB produced.
- NEW: Download the entire term's content in MS Word document format (1-year plan only)
- The complete lesson note and evaluation questions for this topic
- The complete lessons for the subject and class (First Term, Second Term & Third Term)
- Media-rich, interactive and gamified content
- End-of-lesson objective questions with detailed explanations to force mastery of content
- Simulated termly preparatory examination questions
- Discussion boards on all lessons and subjects
- Guaranteed learning